ANOVA
Xavier La Rochelle
2023-11-22
Important : Ce guide assume que vous savez comment :
- Rédiger un script
RMarkdown
- Installer et activer des packages
- Importer une base de données
- Préparer des données
- Vérifier la normalité (Section 1.1)
Vous pouvez cliquer sur les liens ci-dessus pour consulter les guides associées.
0.1 Banque de données
Dans ce guide, nous étudierons des fleurs. La banque de données que
nous utiliserons (iris) est inclue par défaut dans R. Pour
suivre, vous n’avez donc qu’à utiliser la syntaxe suivante :
# Packages
library(knitr)
library(tibble)
library(ggplot2)
library(car)
library(effectsize)
library(emmeans)
# Importer les données
data("iris")
df <- tibble(iris)Voici à quoi devrait ressembler votre banque de données après l’étape de préparation :
df## # A tibble: 150 × 5
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## <dbl> <dbl> <dbl> <dbl> <fct>
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosa
## 7 4.6 3.4 1.4 0.3 setosa
## 8 5 3.4 1.5 0.2 setosa
## 9 4.4 2.9 1.4 0.2 setosa
## 10 4.9 3.1 1.5 0.1 setosa
## # … with 140 more rows1 ANOVA
1.1 Hypothèses
L’hypothèse alternative est qu’il existe au moins une distribution
dont la moyenne s’écarte des autres moyennes : \[
\begin{aligned}
H_0 & : \mu_1 = \mu_2 = \mu_3 = \mu \\
H_1 &: \exists(i,j) \: \text{tel que} \: \mu_i ≠ \mu_j \\
\end{aligned}
\] Note: l’hypothèse \(H_1\) se traduit comme suit : « Il
existe une combinaison de i et j tel que la moyenne \(\mu_i\) n’est pas égale à la moyenne \(\mu_j\) » (shoutout à cet
article wikipedia). Autrement dit, une ANOVA significative nous
indique qu’au moins une des affirmations suivantes est vraie :
\[
\begin{aligned}
\mu_{\text{setosa}} & ≠ \mu_{\text{versicolor}} \\
\mu_{\text{setosa}} & ≠ \mu_{\text{virginica}}\\
\mu_{\text{versicolor}} & ≠ \mu_{\text{virginica}}\\
\end{aligned}
\]
Voici un graphique pour visualiser l’analyse que nous allons effectuer :
ggplot(df, aes(x = Petal.Length, fill = Species)) +
geom_density(alpha = .5) +
geom_vline(lty = 2, col = "red", xintercept = mean(df[df$Species == "setosa",]$Petal.Length)) +
geom_vline(lty = 2, col = "green", xintercept = mean(df[df$Species == "versicolor",]$Petal.Length)) +
geom_vline(lty = 2, col = "blue", xintercept = mean(df[df$Species == "virginica",]$Petal.Length)) +
labs(x = "Longeur du sépale", y = "Densité") +
theme_classic()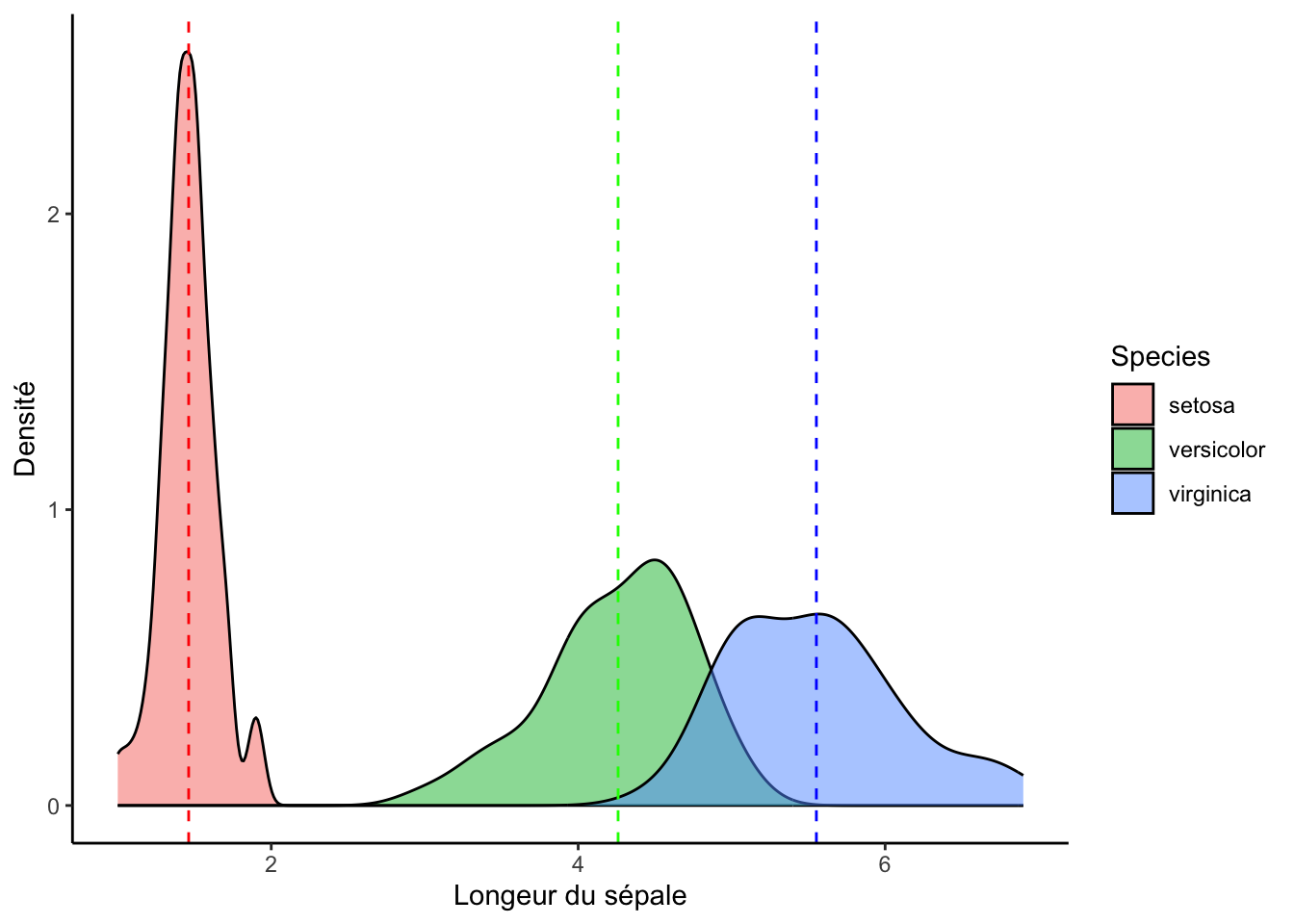
1.2 Postulats
- La variable est continue : ☑
- Les observations sont indépendantes : ☑
- Distribution normale dans chaque groupe : à vérifier
- Homoscédasticité : à vérifier
df_setosa <- subset(df, df$Species == "setosa")
df_versicolor <- subset(df, df$Species == "versicolor")
df_virginica <- subset(df, df$Species == "virginica")1.2.1 Normalité
1.2.1.1 Shapiro-Wilk
shapiro.test(df_setosa$Petal.Length)##
## Shapiro-Wilk normality test
##
## data: df_setosa$Petal.Length
## W = 0.95498, p-value = 0.05481shapiro.test(df_versicolor$Petal.Length)##
## Shapiro-Wilk normality test
##
## data: df_versicolor$Petal.Length
## W = 0.966, p-value = 0.1585shapiro.test(df_virginica$Petal.Length)##
## Shapiro-Wilk normality test
##
## data: df_virginica$Petal.Length
## W = 0.96219, p-value = 0.10981.2.1.2 QQplot
qqnorm(df_setosa$Petal.Length)
qqline(df_setosa$Petal.Length)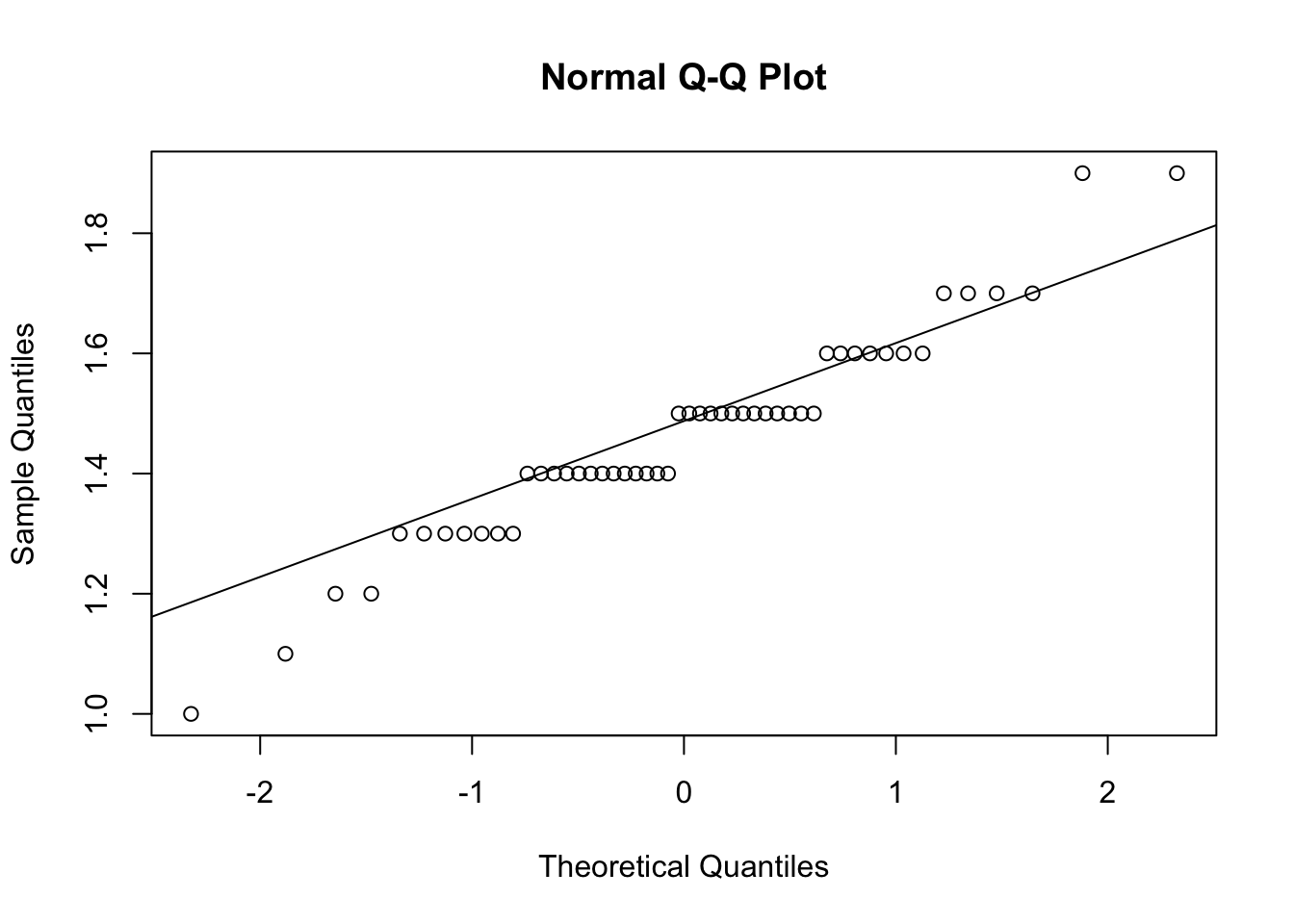
qqnorm(df_virginica$Petal.Length)
qqline(df_virginica$Petal.Length)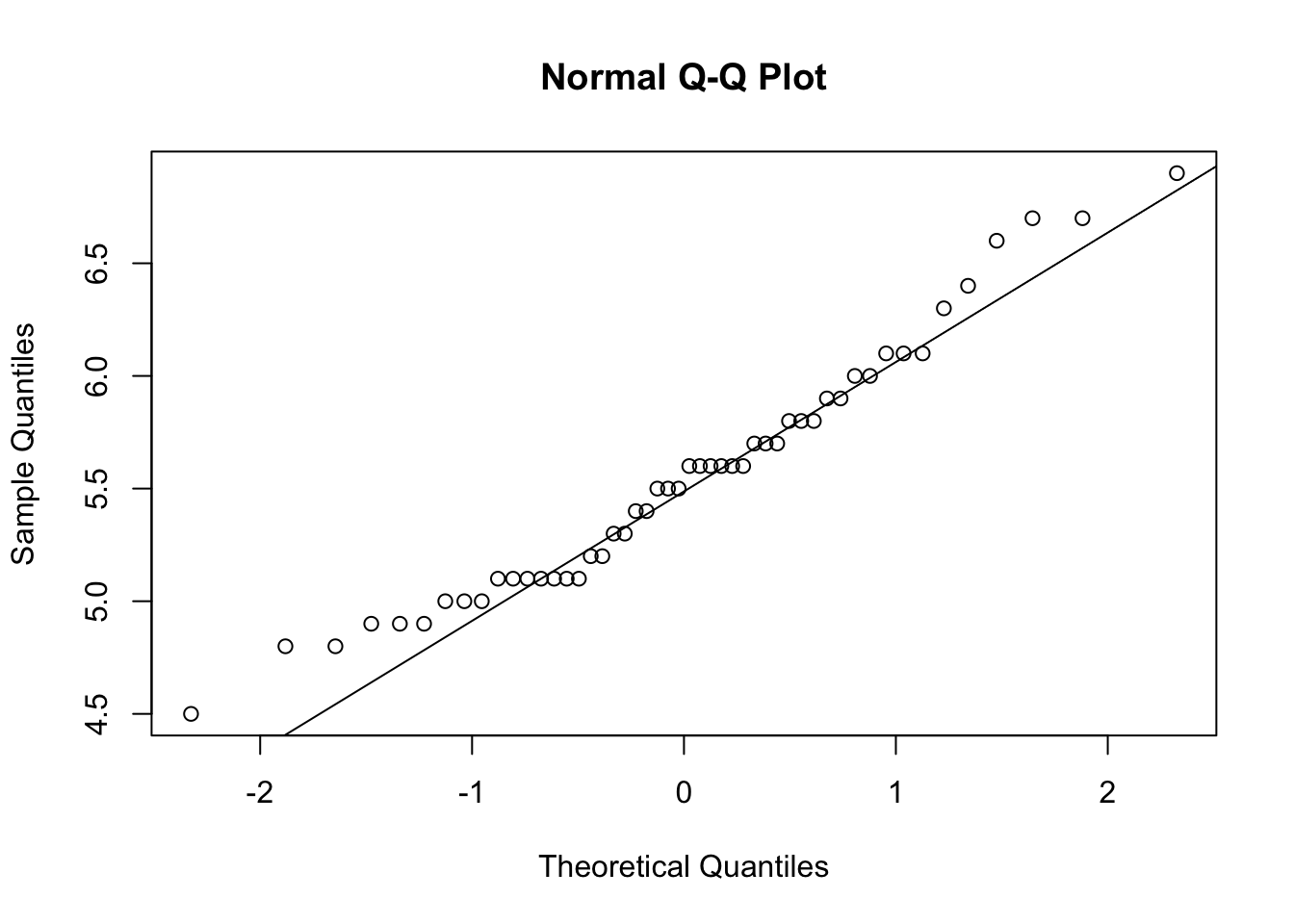
qqnorm(df_versicolor$Petal.Length)
qqline(df_versicolor$Petal.Length)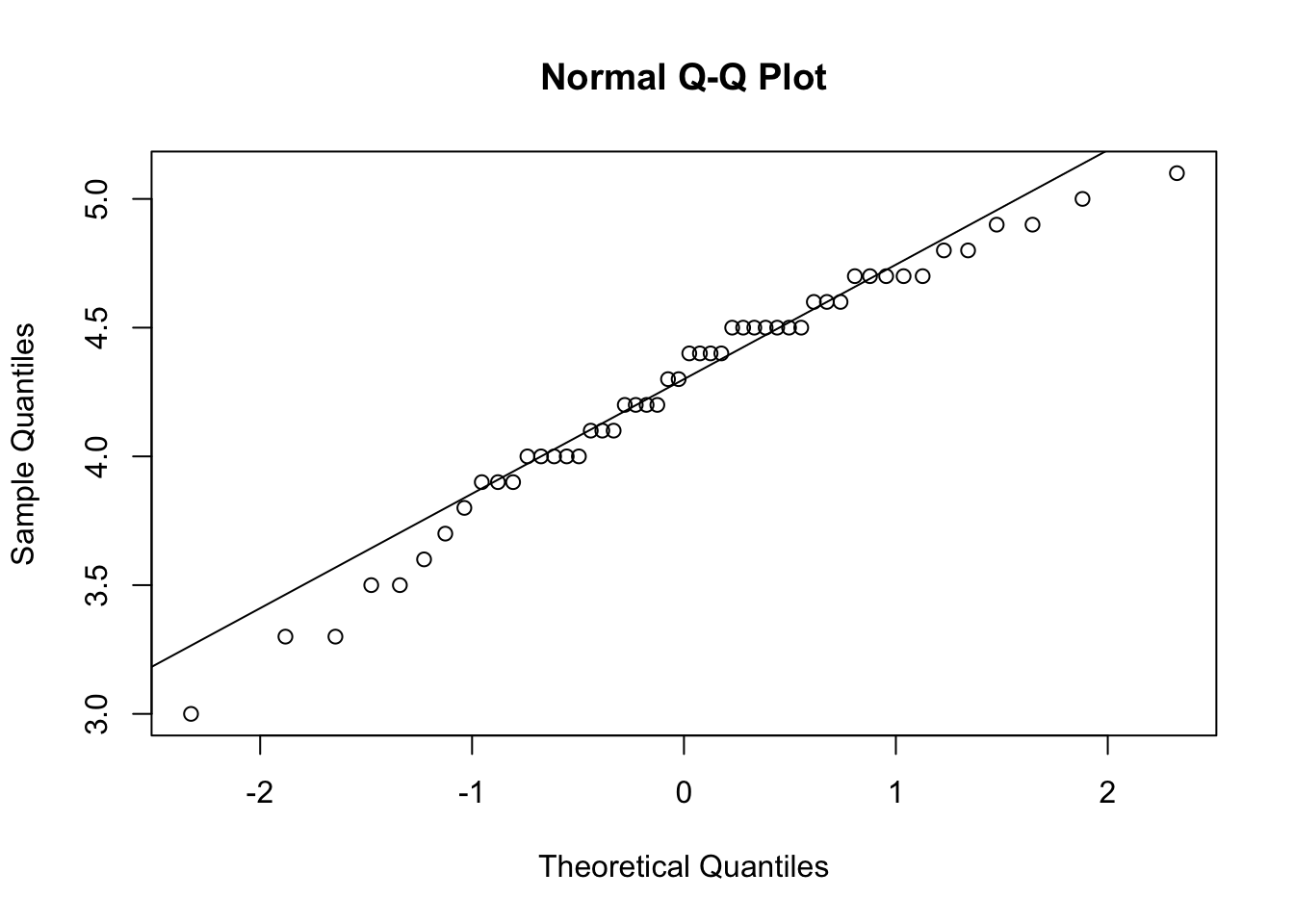
1.2.2 Homoscédasticité
library(car)
leveneTest(df$Petal.Length ~ df$Species)## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 2 19.48 3.129e-08 ***
## 147
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 11.3 Faire le test
model <- lm(Petal.Length ~ Species, data = df)
anova(model)## Analysis of Variance Table
##
## Response: Petal.Length
## Df Sum Sq Mean Sq F value Pr(>F)
## Species 2 437.10 218.551 1180.2 < 2.2e-16 ***
## Residuals 147 27.22 0.185
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On peut conclure que la longueur moyennes des pétales diffère significativement selon l’espèce de fleur (\(F(2,147) = 1180,2; p < ,05\)).
1.4 Calculer la taille d’effet
library(effectsize)
eta_squared(model)## For one-way between subjects designs, partial eta squared is equivalent
## to eta squared. Returning eta squared.## # Effect Size for ANOVA
##
## Parameter | Eta2 | 95% CI
## -------------------------------
## Species | 0.94 | [0.93, 1.00]
##
## - One-sided CIs: upper bound fixed at [1.00].cohens_f(model)## For one-way between subjects designs, partial eta squared is equivalent
## to eta squared. Returning eta squared.## # Effect Size for ANOVA
##
## Parameter | Cohen's f | 95% CI
## -----------------------------------
## Species | 4.01 | [3.60, Inf]
##
## - One-sided CIs: upper bound fixed at [Inf].1.5 Tests post-Hoc
library(emmeans)
emmeans(model, tukey ~ Species)## $emmeans
## Species emmean SE df lower.CL upper.CL
## setosa 1.46 0.0609 147 1.34 1.58
## versicolor 4.26 0.0609 147 4.14 4.38
## virginica 5.55 0.0609 147 5.43 5.67
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## setosa - versicolor -2.80 0.0861 147 -32.510 <.0001
## setosa - virginica -4.09 0.0861 147 -47.521 <.0001
## versicolor - virginica -1.29 0.0861 147 -15.012 <.0001
##
## P value adjustment: tukey method for comparing a family of 3 estimates2 Test de Kruskal-Wallis
Le test de Kruskal-Wallis est souvent présenté comme une version
« robuste » de l’ANOVA et constitue une généralisation du Test U
Mann-Whitney (voir section 2 du guide test-t.html).
2.1 Postulats
Voici les postulats du test de Kruskal-Wallis :
- La variable est continue : ☑
- Les observations sont indépendantes : ☑
2.2 Faire le test
kruskal.test(df$Petal.Length ~ df$Species)##
## Kruskal-Wallis rank sum test
##
## data: df$Petal.Length by df$Species
## Kruskal-Wallis chi-squared = 130.41, df = 2, p-value < 2.2e-16On peut encore une fois conclure que la longueur moyenne des pétales diffère significativement selon l’espèce de fleur (\(\chi^2(2) = 130,4; p < ,05\)).
2.3 Tests post-Hoc
pairwise.wilcox.test(df$Petal.Length, df$Species,
p.adjust.method = "bonferroni")##
## Pairwise comparisons using Wilcoxon rank sum test with continuity correction
##
## data: df$Petal.Length and df$Species
##
## setosa versicolor
## versicolor < 2e-16 -
## virginica < 2e-16 2.7e-16
##
## P value adjustment method: bonferroniNote: Le critère d’ajustement de la valeur de p de Tukey
n’est pas disponible pour cette méthode. J’utilise donc la méthode de
correction de Bonferroni. D’autres méthodes sont disponibles. Pour les
consulter, exécuter le code suivant dans la console :
?p.adjust.methods
Le test post-hoc avec correction de Bonferroni indique que toutes les différences sont significatives (\(p < ,05\)).